刘冰冰1，王明雨1，高洪涛2，张少君1
（1. 山东交通学院 船舶与轮机工程学院，山东 威海 264310；2. 大连海事大学 轮机工程学院，辽宁 大连 116026）
摘要：为探索溴化锂溶液气泡泵的工作机理，在Inamuro大密度比两相流的格子Boltzmann自由能模型的基础上，以时间邻点替代空间邻点，将参数控制的差分项引入相变的分布函数if中，利用二阶迎风差分求解一阶偏导数，利用十四点中心差分格式求解二阶偏导数，将改进模型可模拟的两相流密度比从1000提高到3000，扩展并增强采用格子Boltzmann方法模拟大密度比多相流问题的适应性。通过模拟实际工况下气液密度比为2778的气泡泵垂直管中溴化锂溶液内并排多气泡的上升过程和聚并行为，获得不同初始条件下多气泡的密度场、速度矢量分布图，并对多气泡的运动规律进行分析和总结。研究结果表明，气泡在上升过程中的相互吸引作用和相互排斥作用与气泡群内的气泡大小及其初始位置有关，且气泡间聚并临界距离随着气泡直径的增大或气泡数量的增加而减小。
关键词：格子Boltzmann方法；气泡群；运动过程
溴化锂吸收式制冷系统可利用船舶余热来提高能源利用率，配置该系统是船舶节能减排的有效措施。在研制新型船舶吸收式制冷系统时，利用气泡泵替代传统的机械泵，既可保证溶液泵在吸收式制冷循环中的作用，又可进一步将低品质的热量（船舶余热）用于热源驱动[1]，从而避免对高品位电能产生依赖及对工质的腐蚀性产生影响。因此，无泵化研究越来越受到人们的关注[2]。
气泡泵的性能和工作效率主要由溴化锂溶液两相流的流型及转变特性决定，而在两相流流型研究中，多气泡的碰撞融合过程对两相流的流型转换有决定性影响。有关气泡动力学研究，一些学者已在理论分析、试验研究和数值模拟等方面开展大量工作。HARTUNIAN等[3]研究气泡在不同液体中的稳定性和行为特性；WALTERS等[4]探讨气泡在非黏性液体中的形成机理和气泡形成之后的运动情况；LI等[5]研究流道尺寸对气泡运动行为的影响；JU等[6]借助高速摄像技术对静水中上升气泡沿倾斜壁面的运动特性进行试验研究。以上研究均为有效的理论研究方法，但在不同的试验条件下气泡的运动行为会有很大差异，且有时试验比较复杂，因此利用数值模拟方法来研究气泡的运动行为很重要。DIJKHUIZEN等[7]采用 Front Tracking方法对作用在单个气泡上的上升力进行专门的模型试验和数值模拟研究；RABHA等[8]对单个气泡和群气泡在剪切液体中的上升运动特性及浮力在高黏性液体和低黏性液体中对气泡运动的影响进行数值模拟研究；GONG等[9]采用 VOF模型对矩形流道内单气泡及双气泡的运动进行模拟，分析上下分布的气泡会发生聚并现象；PENG等[10]采用VOF模型模拟不同初速度和不同初始直径的气泡在不同密度矿浆中的运动过程，发现浮生气泡的最佳尺寸随着矿浆密度的增大而减小；WANG等[11]以邻近气泡次级声辐射影响之后的球形气泡径向振动模型为基础，数值模拟研究平面声波场中不同尺寸的 2个气泡的径向振动和平动规律；HE等[12]采用 Level-Set方法数值模拟单个气泡在浮力作用下的上升运动，探讨气泡的初始形状对气泡的变形和上升速度的影响及气泡在不同黏性液体中的生长过程。
上述研究主要集中在气泡的大小及个数对溶液中气泡上升运动的影响上，而多气泡的聚并行为能显著改变流场结构和气-液两相界面，进而深刻影响整个体系的特性，尤其是关于高密度比的溴化锂水溶液与水蒸气气泡间的两相作用的研究对提升气泡泵的工作性能有重要意义。为探索溴化锂溶液气泡泵的工作机理，本文从研究溴化锂水溶液中气泡的运动特性入手，改进格子Boltzmann自由能模型，对并排多气泡的上升过程和聚并行为进行研究，给出溴化锂溶液中水蒸气并排双气泡、3气泡的气泡临界聚并距离，同时模拟不同初始设置的4气泡、6气泡和9气泡的运动过程，讨论气泡数量对临界聚并距离的影响，为流型间转换机制研究提供参考。
本文改进INAMURO等[13]的大密度比的格子Boltzmann自由能模型，在模拟相变的分布函数if时，引入参数控制的差分项，以时间邻点替代空间邻点，可在界面定义中降低人工剪切造成的误差，并可在参数选取合适的情况下将模型的精度提高到二阶精度。
式(1)中：Δx为格子间距；Δt为时间步长；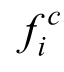
为粒子平衡态分布函数； ci为离散速度；
其中fτ为无量纲松弛时间。
对于速度分布函数ig，在演化方程中考虑气泡浮力的因素，将浮力引入到分布函数的控制方程中（最后一项），即
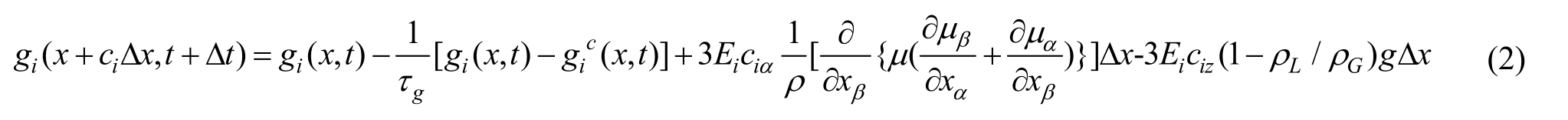
式(2)中：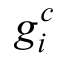
为粒子平衡态分布函数。用来区分两相的序参数和流体预测速度的计算式可表示为
平衡态分布函数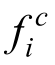
和
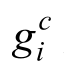为
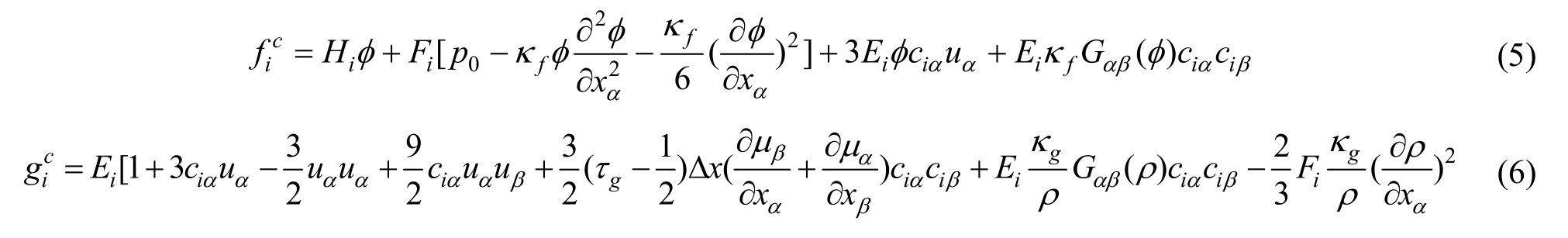
提高差分格式的精度是提高模型数值稳定性的有效方法，采用二阶迎风差分求解一阶偏导数，可获得较准确的解，具有二阶精度误差，且绝对稳定。在原模型的基础上利用十四点差分格式求解二阶偏导数，可提高模拟大密度比多相流问题的适应性。
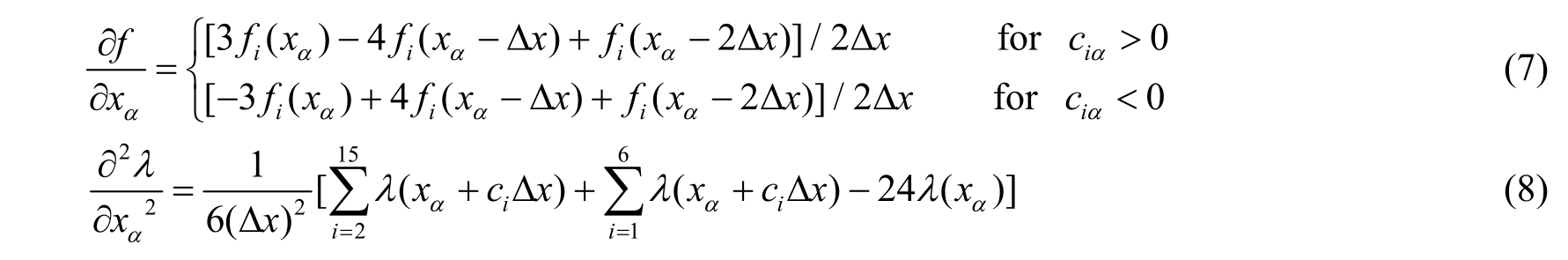
为验证改进大密度比自由能模型程序的有效性，模拟文献[14]中单气泡的最终形状及流场分布。图 1为单气泡上升的最终形状密度云图和速度矢量图与文献图[14]的对比，在其他计算参数相同的情况下，由于文献[14]中只给出气液黏度比，并未给出气液黏度取值，且该黏度参数是自行确定的，故二者略有差异，但模拟结果大体上相似，此足以证明程序的有效性。
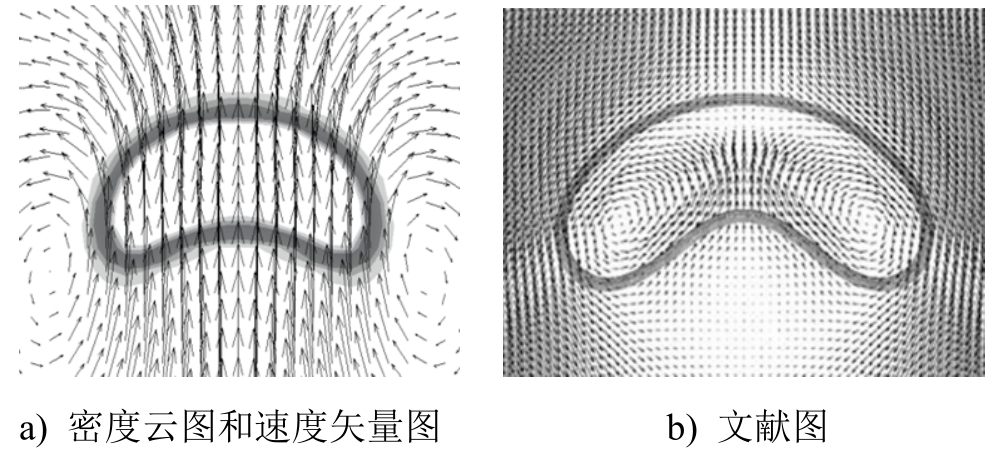
图1 单气泡形状对比
在溴化锂吸收式制冷试验中，气泡泵发生器的发生温度为110℃，此时浓度为57.5%的溴化锂溶液的密度为1614.7kg/m3，动力黏度为1.7Pa·s，水蒸气密度为0.58kg/m3，动力黏度为0.218Pa·s。为模拟气泡泵提升管，采用48×48×96立方体格子区域，对应模拟管径为4.8mm的垂直上升玻璃管，密度比为2778。模拟单气泡在管内溴化锂溶液中的上升过程（见图2a）），并与试验中利用高速摄像机所拍摄的单气泡的运动形态（见图2b））相对比，两者一致，可验证模型的准确性和可靠性。
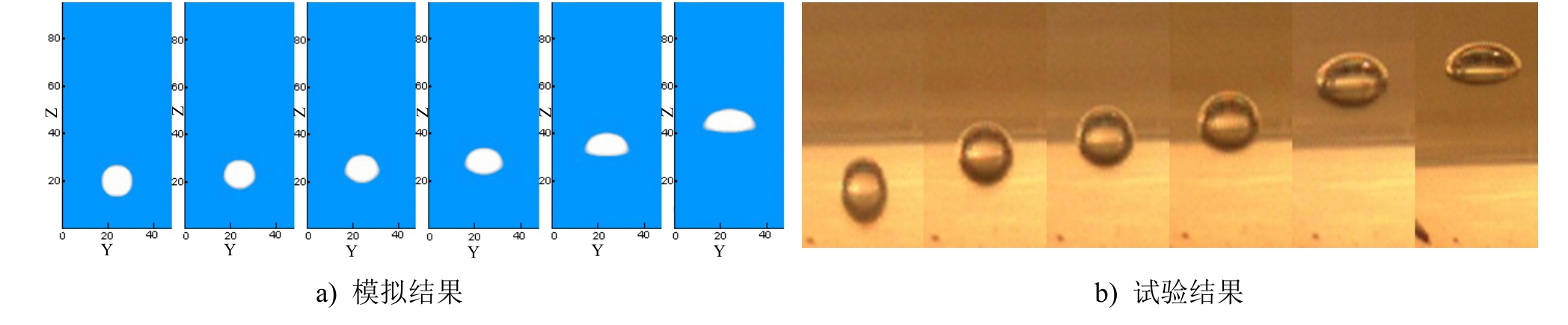
图2 单气泡上升过程模拟和试验对比
并排气泡相互作用存在吸引和排斥2种情况，设置2个大小相同、初始直径为格子步长12的水平并排气泡，其圆心间初始距离为格子步长16。见图3为并排双气泡上升分离密度与速度矢量分布，双气泡在上升过程中，出现靠近和分离2个阶段。第一阶段两气泡在初始上升时，气泡间产生的低压区使得两气泡相互靠近，此时两气泡间的作用力为引力；第二阶段随着两气泡的上升，气泡底部左右两侧流场会出现2个漩涡，气泡间距离逐渐减小，而双气泡的速度持续增大，此时气泡表面漩涡开始起主导作用，两气泡间的漩涡方向相反，导致两气泡相互分离。
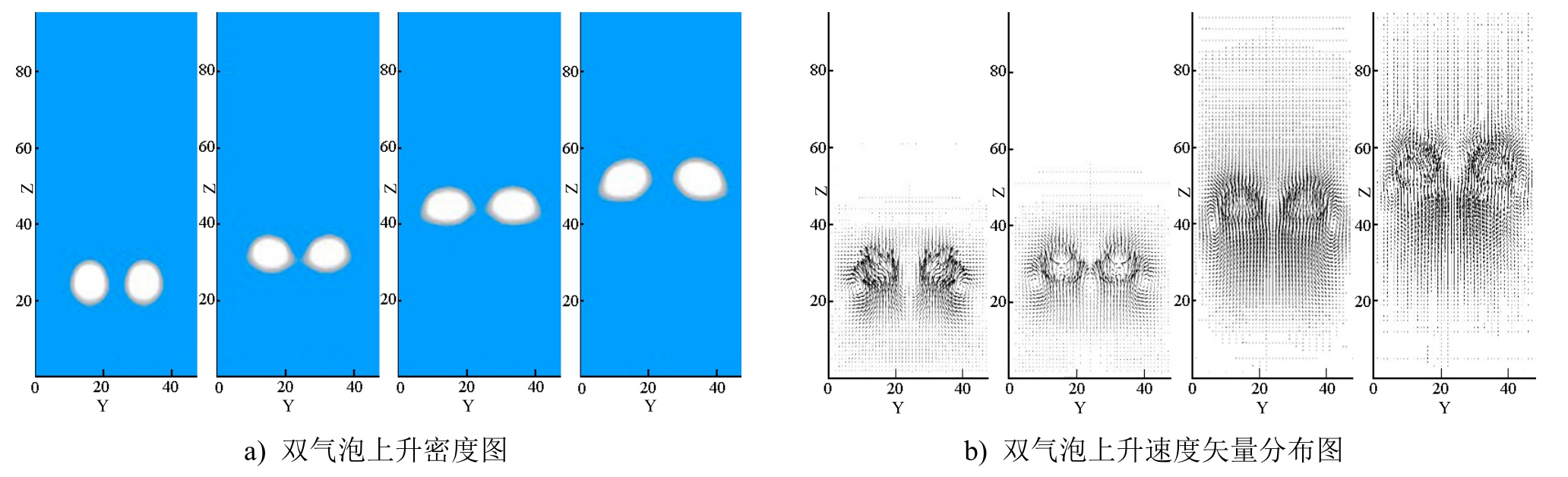
图3 并排双气泡上升分离密度与速度矢量分布
当设置两并排的大小相同的气泡在初始状态下的直径为格子步长 10，圆心间初始距离为格子步长 12时，两气泡的运动过程见图4。两气泡在上升时首先相互靠近并发生接触；接着水平气泡间形成气桥，两气泡连为一体；最后气桥在竖直方向上迅速扩张，两气泡融为一体。融合之后的气泡长度逐渐缩短，呈扁平的盘状。由速度矢量分布可知，无论并排双气泡最后是发生聚并还是分离，两气泡周围的流场都在水平方向上起排斥作用。
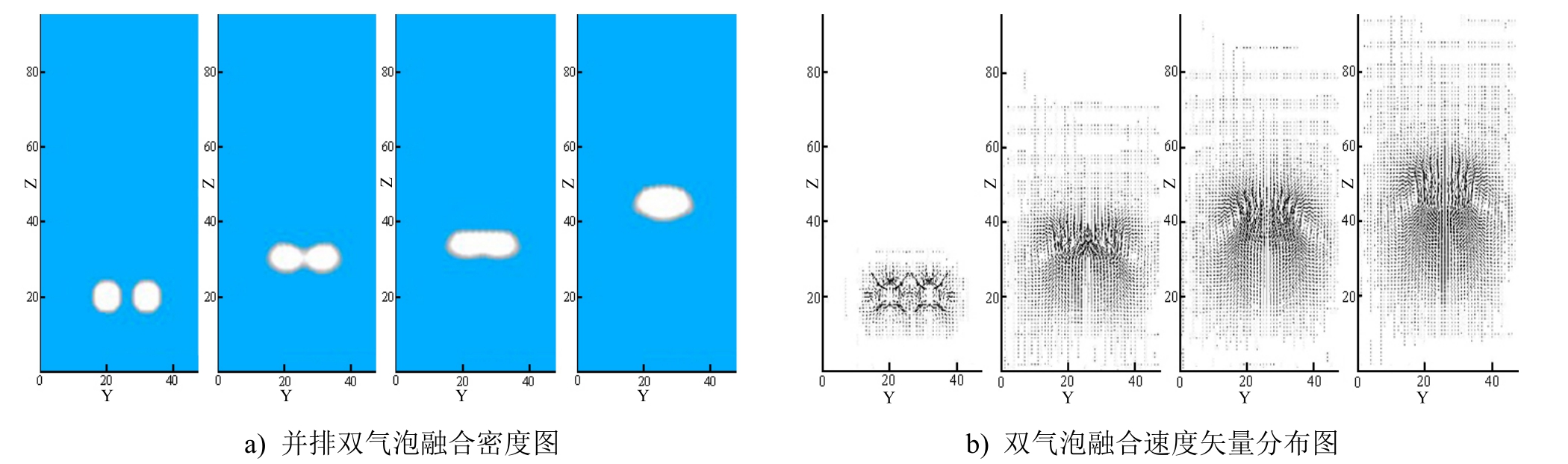
图4 并排双气泡上升融合密度与速度矢量分布
图 5给出采用Volume of fluid方法模拟的水平并排气泡的运动过程[15]。虽然其物性条件与本文有一定差异，但可对气泡水平运动过程进行定性比较。在不同的初始条件下，并排双气泡可能出现2种不同的运动情况，即先靠近再分离或聚并融合。
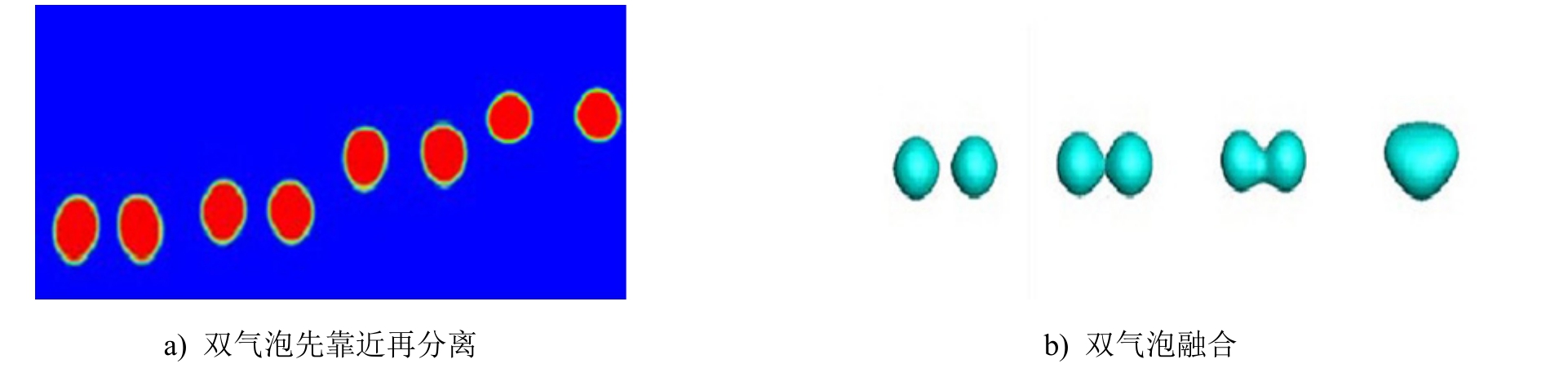
图5 并排双气泡运动过程文献[15]模拟结果
为研究3气泡的上升过程，设置大小相同，直径为格子步长6，相互间初始距离为格子步长16的3个圆形气泡（见图6）。在这种情况下，3气泡各自独立上升，且运动过程中的形态变化与单气泡相似，但气泡在上升过程中未发生水平方向上的运动，相对的初始水平位置没有发生改变。出现这种情况的原因是初始气泡直径较小，初始水平距离较大，致使气泡间的流场影响很小，加上气泡为对称放置的，左右两气泡对中间气泡流场的影响相互抵消，因此出现3气泡并排独立上升的过程。
设置大小相同，直径为格子步长10，相互间初始距离为格子步长12的3个圆形气泡（见图7）。在该情况下，气泡在上升过程中发生碰撞并融合：在气泡上升初期，3气泡同时发生形变，变成椭球形，且中间气泡的水平位置不变，而左右两气泡分别向中间靠拢；在与中间气泡碰撞时，左右两气泡没有破碎，而是与中间气泡融合成一个扁长的大气泡继续上升。
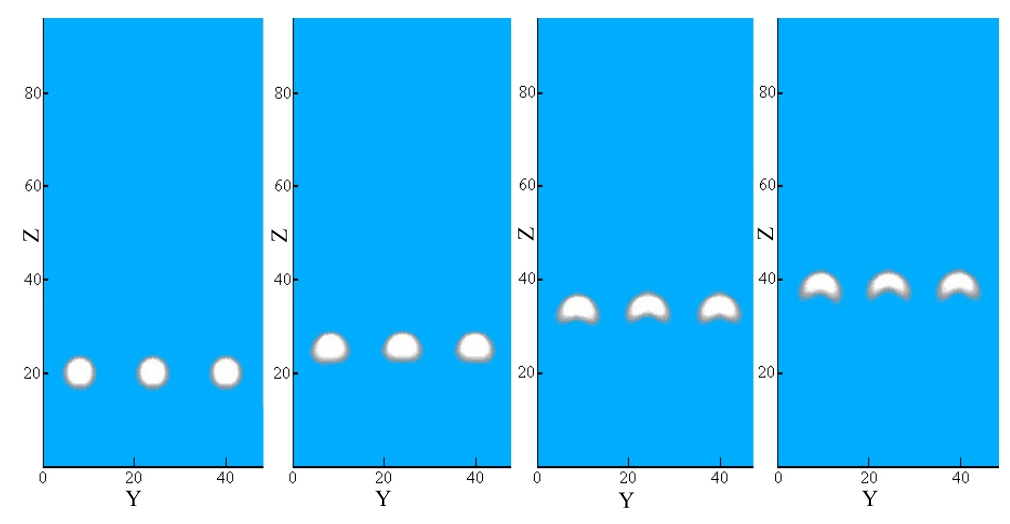
图6 3气泡独立运动密度与速度矢量分布
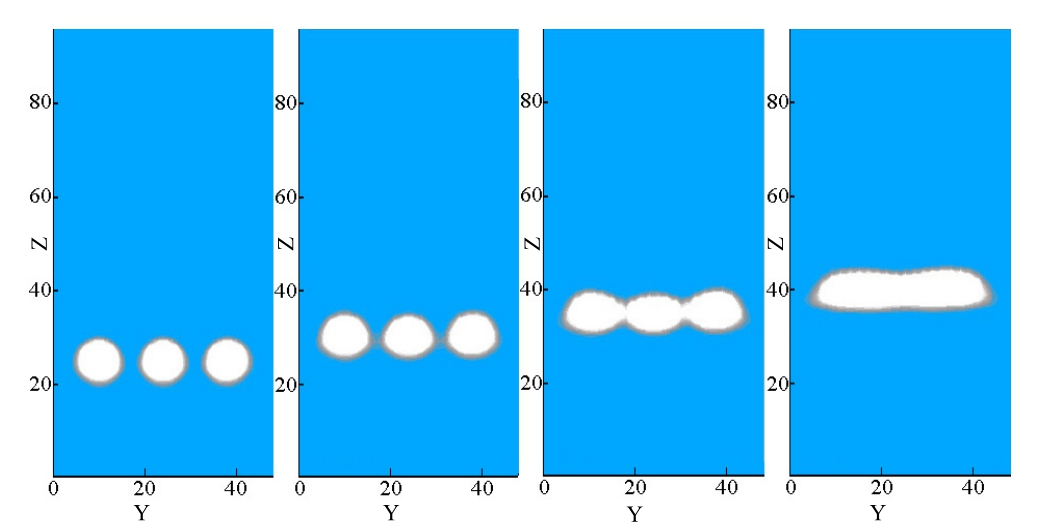
图7 3气泡运动融合过程密度与速度矢量分布
由模拟结果可知，气泡在上升过程中存在吸引的作用：当气泡间距离较小时，气泡运动的惯性起主导作用；当气泡周围流场的漩涡所起的排斥作用不足以导致气泡分离时，气泡迅速发生融合。在液体中自由上升的并排气泡能否发生聚并，与气泡间初始距离、气泡大小、溶液的物理性质和气泡数量等因素有关。因此，为研究气泡在水平方向上能否发生聚并及其与气泡间初始距离和气泡大小的关系，定义气泡聚并的临界距离[15]为
式(9)中：0x为初始时刻气泡圆心之间的水平距离；0d气泡初始直径，对于自由上升的气泡，气泡间存在临界的初始水平间距，当气泡间距离超过临界距离时，气泡不会发生聚并，反之会相互融合。
为研究溴化锂溶液中双气泡和3气泡的聚并临界距离，模拟初始直径为格子步长 4～12的气泡的运动过程（见图8）。由图8可知：随着气泡直径的增大，临界聚并距离减小，这是因为气泡直径的增大会造成流场结构及空间位阻增大，进而使气泡发生聚并的难度增大；球形的小气泡对流体的剪切作用更加明显，使其容易相互靠近并发生聚并；3气泡聚并比双气泡聚并容易发生，这是由于随着气泡个数的增加，气泡间的相互作用增强，使得气泡底部漩涡间排斥力减小，更有利于发生气泡聚并。
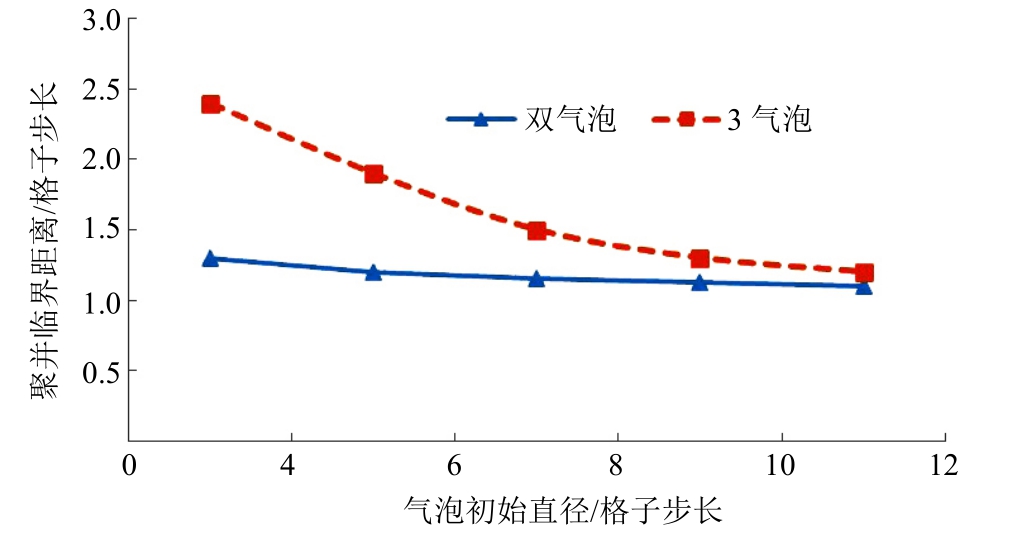
图8 双气泡与3气泡聚并临界距离
对称放置4个大小相同的气泡，若气泡初始直径较小（见图9a）），则底部2个气泡在运动过程中会先发生融合，上面2个气泡分别向左右运动，随后4个气泡相互碰撞连接，先融合成一个长形气泡，再分散成2个小气泡，相互分离。若气泡初始直径较大（见图9b）），则底部2个气泡先发生碰撞，上面2个气泡相互融合，此时两对大气泡的保形能力很弱，流场很不稳定，4个气泡发生接触时破碎。
为研究多气泡的上升运动情况，设置大小相同、直径为格子步长6的6个球形气泡，气泡间距为格子步长16，气泡群在上升过程中既发生竖直方向上的融合，又发生水平方向上的融合。由于上下两排气泡的间距较小，因此在上升过程中首先发生3组竖直方向上双气泡的碰撞和融合（见图10b）），融合之后2个气泡的高度缩短并向中间气泡靠拢，在中间气泡底部两侧，3组融合之后的气泡发生水平方向上的接触（见图10d）），随后接触部分的气桥迅速扩张，最后6个气泡融合成一个大气泡（见图10f）），此时气泡很不稳定，极易在流场的作用下破裂。
图9 4气泡的上升运动过程
设置大小相同的9个气泡分3排放置在提升管内，前2排气泡在上升过程中会首先发生融合，由于在竖直的3气泡中，最底部气泡的尾流会对中间气泡产生向上的引力，而下方气泡的流场也会给中间气泡向上的推力，因此中间排的气泡有较大的速度，首先与上方气泡融合；在继续运动过程中，底部气泡也会与前2排气泡碰撞，由于此时流场极不稳定，多气泡会在接触瞬间破碎（见图11）。
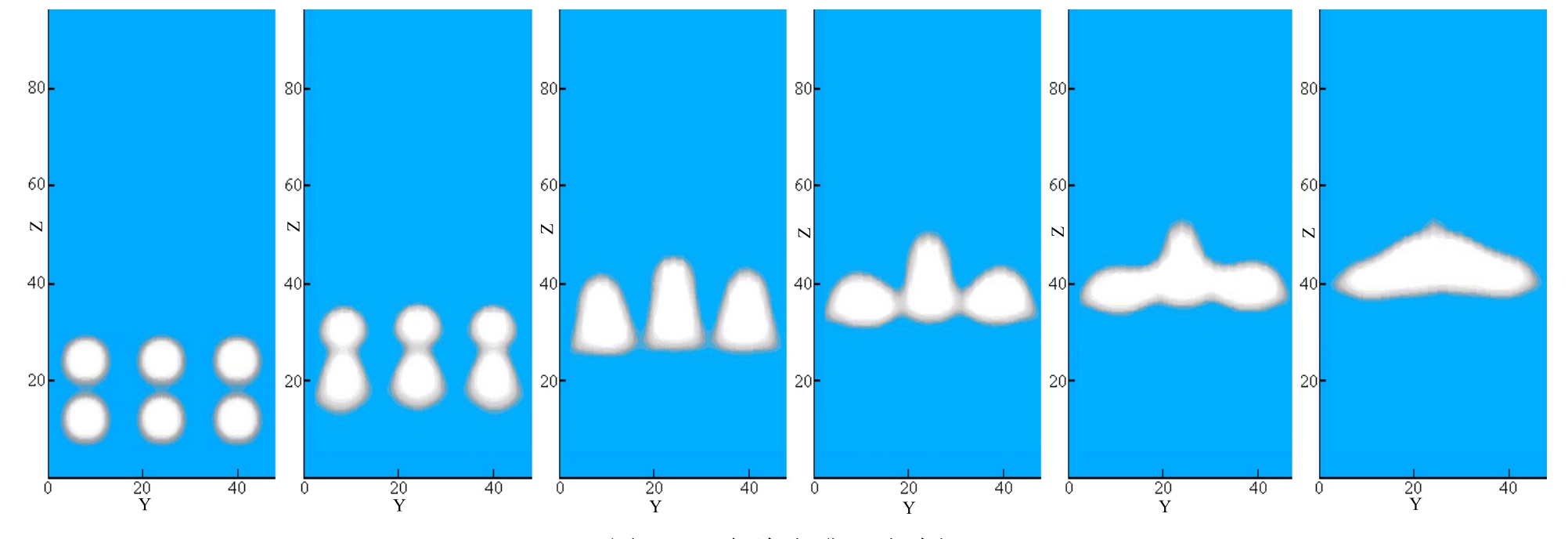
图10 6气泡上升运动过程
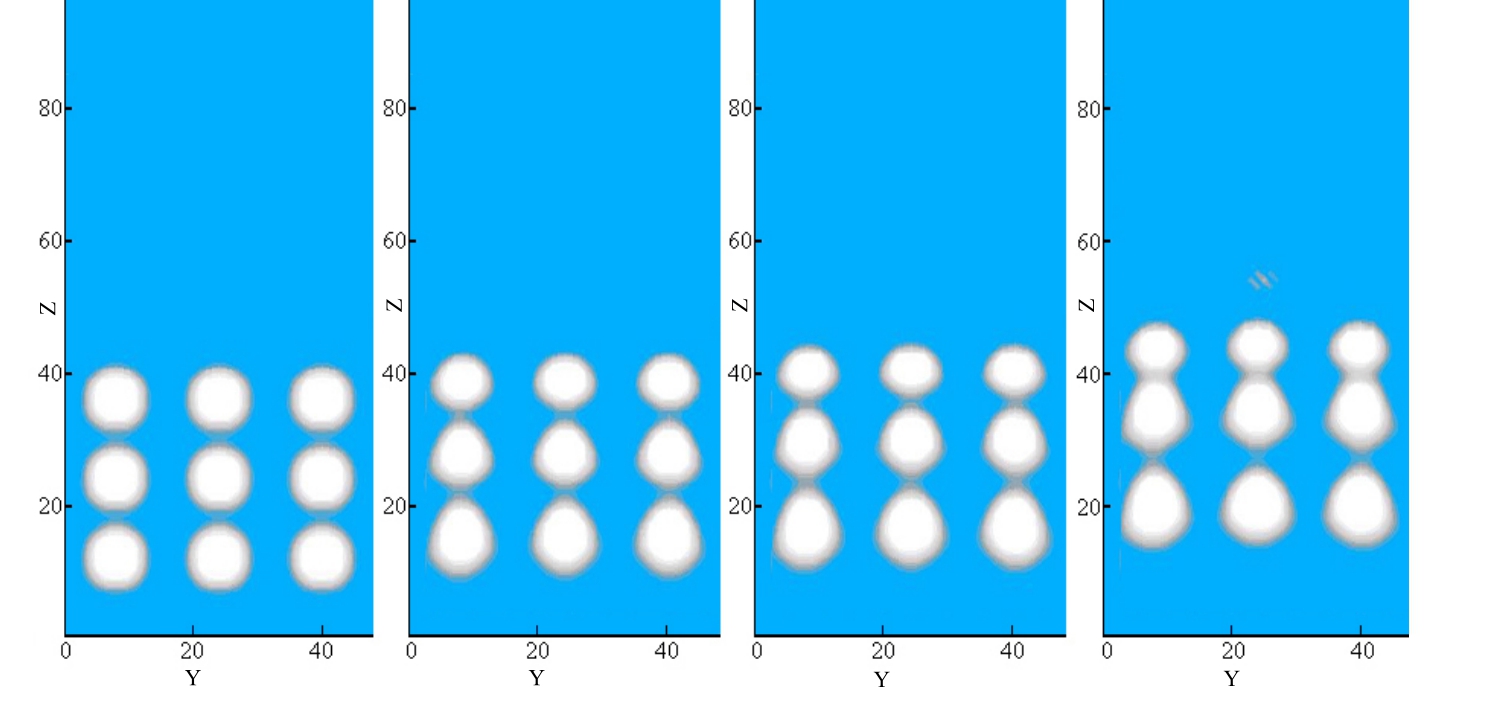
图11 9气泡上升运动过程
在试验工况下采用改进格子Boltzmann方法大密度比自由能模型模拟气泡泵垂直管中溴化锂溶液内并排多气泡的上升过程和聚并行为，得到以下结论：
(1) 在INAMURO[13]的大密度比两相流的格子Boltzmann自由能模型中，以时间邻点替代空间邻点，将参数控制的差分项引入相变的分布函数if中，利用二阶迎风差分格式求解一阶偏导数，利用十四点差分格式求解二阶偏导数，将模型可模拟的两相流密度比从1000提高到3000；
(2) 气泡在上升过程中扰动周围流场，对其他气泡既有相互吸引作用也有相互排斥作用，这与气泡群内气泡的大小和初始位置有关；
(3) 随着气泡直径的增大，聚并临界距离减小，这是由于气泡直径的增大会造成流场结构及空间位阻增大，进而使气泡发生聚并的难度增大；
(4) 随着气泡个数的增加，气泡间相互作用增强，使得气泡底部漩涡间排斥力减小，更有利于发生气泡聚并，即随着气泡直径的增大或气泡数量的增加，气泡间聚并临界距离减小。
【 参 考 文 献 】
[1] HOFFMANN L, GREITER I, WANGER A, et al. Experimental investigation of heat transfer in a horizontal tube falling film absorber with aqueous solutions of LiBr with and without surfactants [J]. Refrig, 1996 (19): 331- 341.
[2] BENHMIDENE A, CHAOUACHI B, GABSI S. A review of bubble pump technologies [J]. Journal of Applied Sciences, 2010,10(16):1806-1813.
[3] HARTUNIAN RA, SEARS W. On the instability of small gas bubbles moving uniformly in various liquids [J]. Journal of Fluid Mechanics, 1957, 3(1):27-47.
[4] WALTERS J, DAVIDSON J. The initial motion of a gas bubble formed in an inviscid liquid [J]. Journal of Fluid Mechanics,1963, 17(3):321-336.
[5] LI WZ, ZHAO DY, CHEN GJ. A numerical simulation on effects of vertical channel wide on deformation and heat transfer of a rising gas bubble [J]. Chinese Journal of Computational Mechanics, 2006, 23(2):196-201.
[6] JU H, CHEN G, LI GD, et al. Experimental study on motion behavior of single bubble rising along inclined plane in still water [J]. Chinese Journal of Hydrodynamics, 2011, 26(3): 327-332.
[7] DIJKHUIZEN W, VAN SAM, KUIPERS JAM. Numerical and experimental investigation of the lift force on single bubbles [J].Chemical Engineering Science, 2010, 65(3): 1274-1287.
[8] RABHA S, BUWA V. Volume-Of-Fluid (VOF) simulations of rise of single/multiple bubbles in sheared liquids [J]. Chemical Engineering Science, 2010, 65(1): 527-537.
[9] GONG DX, HUANG SF, WANG K, et al. The study on mechanism of bubble motion in rectangular channel by CFD [J].Nuclear Power Engineering, 2014, 35(3):111-116.
[10] PENG XQ, CHEN SC, SONG YP, et al. Numerical simulation of flotation bubble motion in suspension fluid [J]. The Chinese Journal of Nonferrous Metals, 2013, 23(11):3232-3237.
[11] WANG CH, LIN SY. The coupled motion of bubbles in ultrasonic field [J]. Acta Acustic, 2011, 36(3): 325-331.
[12] HE D, LI YP, LIU YY. Effect of initial bubble shape on dynamics of a buoyancy-driven bubble [J]. Journal of Xi’an Jiaotong University, 2011, 45(1): 43-47.
[13] INAMURO T, OGATA T, TAJIMA S, et al. A lattice Boltzmann method for incompressible two-phase flows with large density differences [J]. Journal of Computational Physics 2004, 19(8): 628-644.
[14] INAMURO T, OGATA T, OGINO F. Numerical simulation of bubble flows by the lattice Boltzmann method [J]. Future Generation Computer Systems, 2004, 20(6):959-964.
[15] 刘静如. 非牛顿流体中多气泡相互作用、聚并与破裂过程的数值模拟[D]. 天津：天津大学, 2014.
Analysis on the Characteristics of Bubble Group Motion Inside Bubble Pump Riser
LIU Bing-bing1，WANG Ming-yu1，GAO Hong-tao2，ZHANG Shao-jun1
（1. College of Naval Architecture and Marine Engineering, Shandong Jiaotong University, Weihai 264310, China;2. Institute of Marine Engineering, Dalian Maritime University, Dalian 116026, China）
Abstract:In order to study the working mechanism of lithium bromide bubble pump, two-phase flow lattice Boltzmann free energy model with Inamuro’s large density ratio is taken as the basis where the space neighboring points are replaced by time neighboring points, and the parametrically controlled difference terms are introduced into the phase transitional distribution function fi. The second order upwind difference scheme is used to solve the first order partial terms and the fourteen points central difference scheme is to solve the second order partial terms. Then the simulated two-phase flow density ratio of the enhanced model is increased from 1000 to 3000 for the first time, expanding and improving the adaptability of the lattice Boltzmann method to simulate the large density ratio multi-flow problems. Through simulating the parallel bubbles rising and coalescing in the lithium bromide inside the vertical pipe of the bubble pump with a gas-liquid density ratio of 2778, the bubbles’ density field and velocity vector distribution diagram under different initial conditions are obtained, and the motion patterns of the bubbles are analyzed and summarized. The result shows that the mutual attraction and repelling interactions in between the bubbles are related to the size and initial position of the bubbles in the bubble group. The critical distance of the coalesced bubbles decreases when the diameter or quantity of bubbles increases.
Key words:lattice Boltzmann method; bubble group; motion process
中图分类号：TQ021；U664.8
文献标志码：A
文章编号：2095-4069 (2018) 03-0001-07
收稿日期：2016-07-13
基金项目：国家自然科学基金（50976015; 51609131）；辽宁省科学技术计划项目（2010224002）；交通运输部海事局科技项目（2012_27）；山东省自然科学基金（ZR2014JL038；ZR2017MEE031）
作者简介：刘冰冰，女，博士，1988年生。2017年毕业于大连海事大学轮机工程专业，现从事船舶防污染研究工作。
DOI：10.14056/j.cnki.naoe.2018.03.001